1次元調和振動子の可視化

小出昭一郎『量子力学（Ⅰ）』のp.51にある1次元調和振動子のグラフを再現します。

可視化するのは以下の関数です。

$X_n(x) = \Bigl(\frac{\sqrt{2mw/h}}{2^nn!}\Bigr)^{1/2}H_n\Bigl(\sqrt\frac{mw}{\hbar}x\Bigr)\exp\Bigl(-\frac{mw}{2\hbar}x^2\Bigr)$

この関数は下記の方程式を満たします。

$\Bigl(-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+\frac{mw^2}{2}x^2\Bigr)X(x)=\epsilon_xX(x)$

ディラック定数 $\hbar$ はそのまま使うと都合が悪いので $M=m/\hbar$ とおいて下記の関数を使います。

$X_n(x) = \Bigl(\frac{\sqrt{Mw/\pi}}{2^nn!}\Bigr)^{1/2}H_n\Bigl(\sqrt{Mw}x\Bigr)\exp\Bigl(-\frac{Mw}{2}x^2\Bigr)$

def X(n,M,w):
    A = sqrt(sqrt(w*M/pi)/2^n/factorial(n))

    return lambda x : A*hermite(n,x)*exp(-x^2*M*w/2)

上記プログラムをmain.sageとして保存し、Sage Shellでロードしておきます。

sage: load('main.sage')

n=0

本記事では一貫して $M=w=1$ とします。

sage: plot(X(0,1,1),(-5,5))
Launched png viewer for Graphics object consisting of 1 graphics primitive

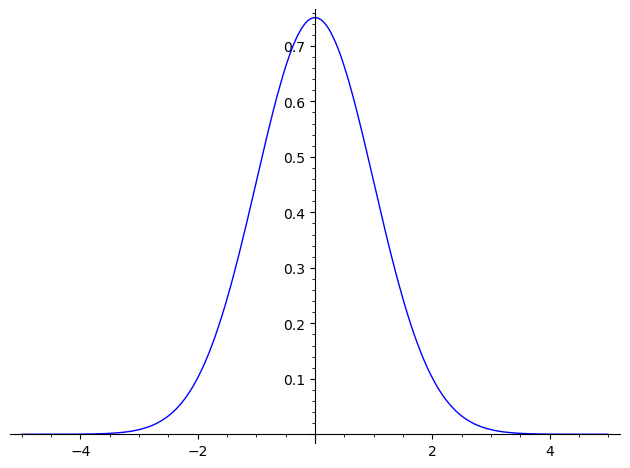
f:id:riverta1992:20201219164619p:plain

n=1

sage: plot(X(1,1,1),(-5,5))
Launched png viewer for Graphics object consisting of 1 graphics primitive

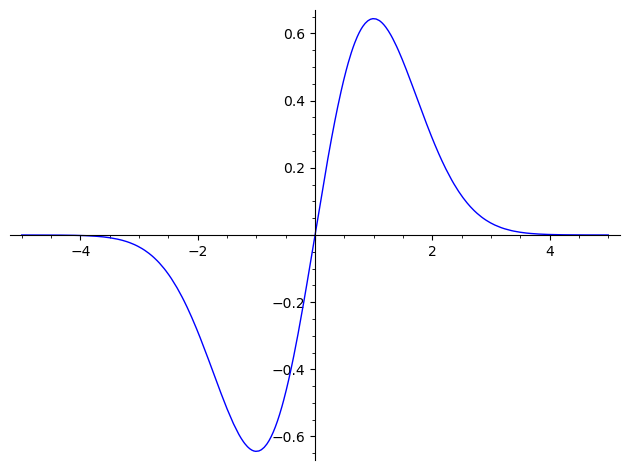
f:id:riverta1992:20201219164742p:plain

n=2

sage: plot(X(2,1,1),(-5,5))
Launched png viewer for Graphics object consisting of 1 graphics primitive

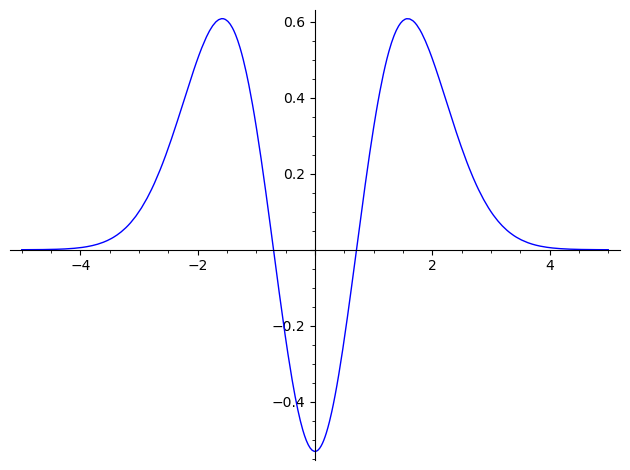
f:id:riverta1992:20201219165225p:plain

n=3

sage: plot(X(3,1,1),(-5,5))
Launched png viewer for Graphics object consisting of 1 graphics primitive

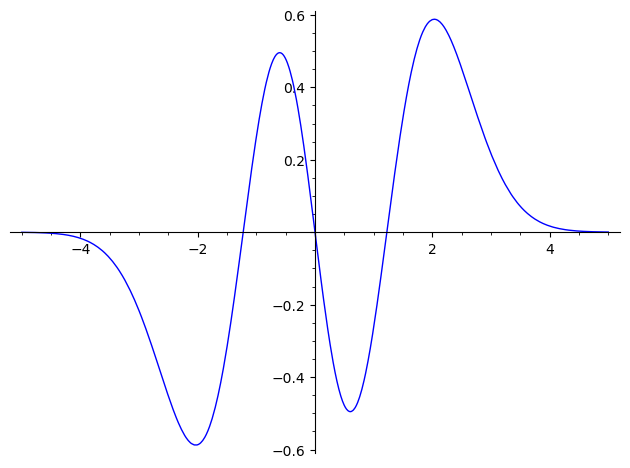
f:id:riverta1992:20201219165312p:plain

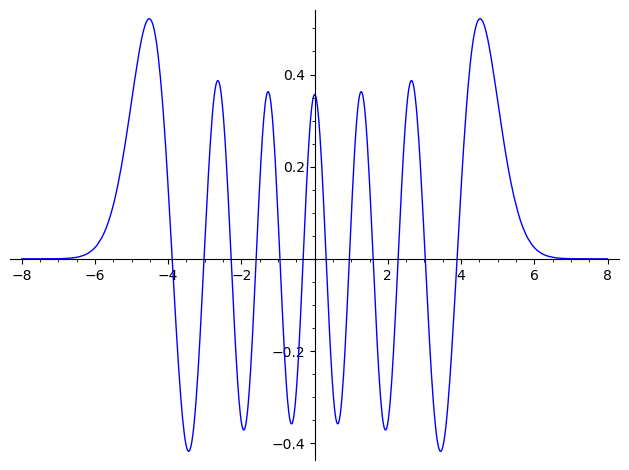
n=12

sage: plot(X(12,1,1),(-8,8))
Launched png viewer for Graphics object consisting of 1 graphics primitive

f:id:riverta1992:20201219165405p:plain

追記1

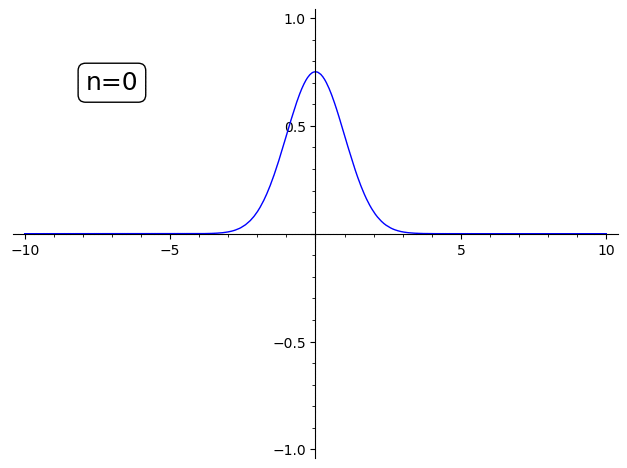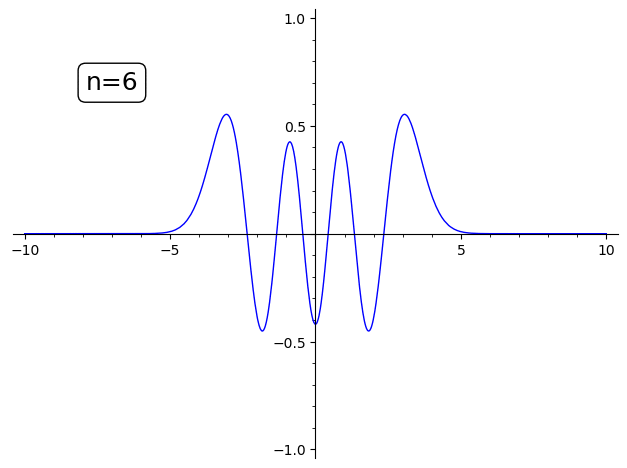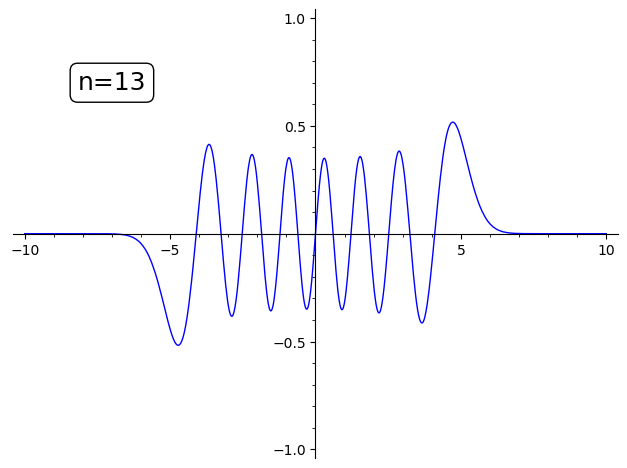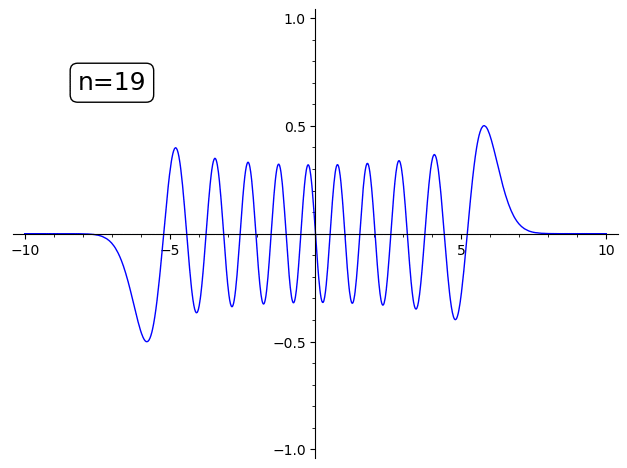
$X_n(x)$ の n を変えてアニメーションにしました。

sage: l = [text("n={}".format(i),(-7,0.7),fontsize=18,color="black",bounding_box={'boxstyle':'round','fc':'w'})+plot(X(i,1,1),(-10,10),ymin=-1,ymax=1) for i in range(20)]
sage: animate(l)
Launched gif viewer for Animation with 20 frames

f:id:riverta1992:20201219183317g:plain

追記２

$X_n(x)$ の2乗を定義する。

def X2(n,M,w):
    A = sqrt(sqrt(w*M/pi)/2^n/factorial(n))

    return lambda x : (A*hermite(n,x)*exp(-x^2*M*w/2))^2

2乗したものは規格化されているから積分すると1になる。sage には numerical_integral という便利なものがあるので n=12 のグラフで数値積分をしてみる。この積分は下の図の灰色部分の面積を表す。

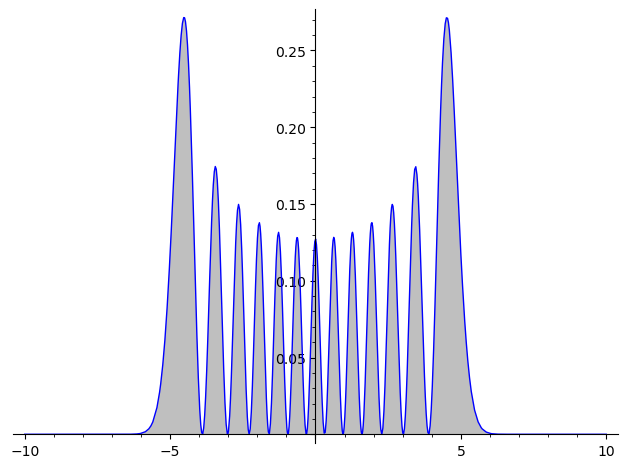
f:id:riverta1992:20201219210837p:plain

x の範囲は本来実数全体にわたるが、数値積分なので-10から10までの積分とした。

単に計算してもつまらないので、これもアニメーションにしてみる。ごちゃごちゃしているが下記に示すプログラムで実行できる。

sage: l = [graphics_array([[plot(lambda x:0.0 if x>a else X2(12,1,1)(x),-10,10,fill=True)+plot(X2(12,
....: 1,1),a,10)],[plot(lambda x:numerical_integral(X2(12,1,1),-10,x)[0],-10,10,plot_points=100)+poin
....: t((a,numerical_integral(X2(12,1,1),-10,a)[0]),size=70,rgbcolor="red")]]) for a in sxrange(-10,1
....: 0,1)]
sage: animate(l)
Launched gif viewer for Animation with 20 frames